olzhere.blogg.se

The difference between the two is simply the factor e j π -a rotation of 180D around the Smith Chart!.

Note this can likewise be expressed as: Γ=ġ− y′ y′ −1 y′ −1 =− = e jπ y′+1 y′+1 1+ y′Ĭontrast this to the mapping between normalized impedance and Γ : We can therefore likewise express Γ in terms of normalized admittance: Γ= Rotation around the Smith Chart Thus, ΓL =

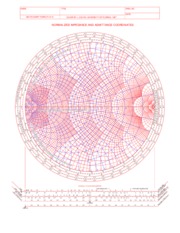
Q: Can we also map these points and contours onto the complex Γ plane? A: You bet! Let’s first rewrite the refection coefficient function in terms of line admittance Y ( z ) : Y − Y (z ) Γ (z ) = 0 Y0 + Y ( z )

Admittance and the Smith Chart Just like the complex impedance plane, we can plot points and contours on the complex admittance plane: Im = G